VJudge--More is better

题目 - More is better

Mr Wang wants some boys to help him with a project. Because the project is rather complex, the more boys come, the better it will be. Of course there are certain requirements.

Mr Wang selected a room big enough to hold the boys. The boy who are not been chosen has to leave the room immediately. There are 10000000 boys in the room numbered from 1 to 10000000 at the very beginning. After Mr Wang’s selection any two of them who are still in this room should be friends (direct or indirect), or there is only one boy left. Given all the direct friend-pairs, you should decide the best way.

Input

The first line of the input contains an integer n (0 ≤ n ≤ 100 000) - the number of direct friend-pairs. The following n lines each contains a pair of numbers A and B separated by a single space that suggests A and B are direct friends. (A ≠ B, 1 ≤ A, B ≤ 10000000)

Output

The output in one line contains exactly one integer equals to the maximum number of boys Mr Wang may keep.

Sample Input

4
1 2
3 4
5 6
1 6
4
1 2
3 4
5 6
7 8

Sample Output

4
2

Hint

A and B are friends(direct or indirect), B and C are friends(direct or indirect), 
then A and C are also friends(indirect).

 In the first sample {1,2,5,6} is the result.
In the second sample {1,2},{3,4},{5,6},{7,8} are four kinds of answers.

题目大意:

A和B是朋友（直接或间接），B和C是朋友（直接或间接），
那么A和C也是朋友（间接）。

在第一个样本{1,2,5,6}中是结果。
在第二个示例{1,2}，{3,4}，{5,6}，{7,8}中有四种答案。

思路：

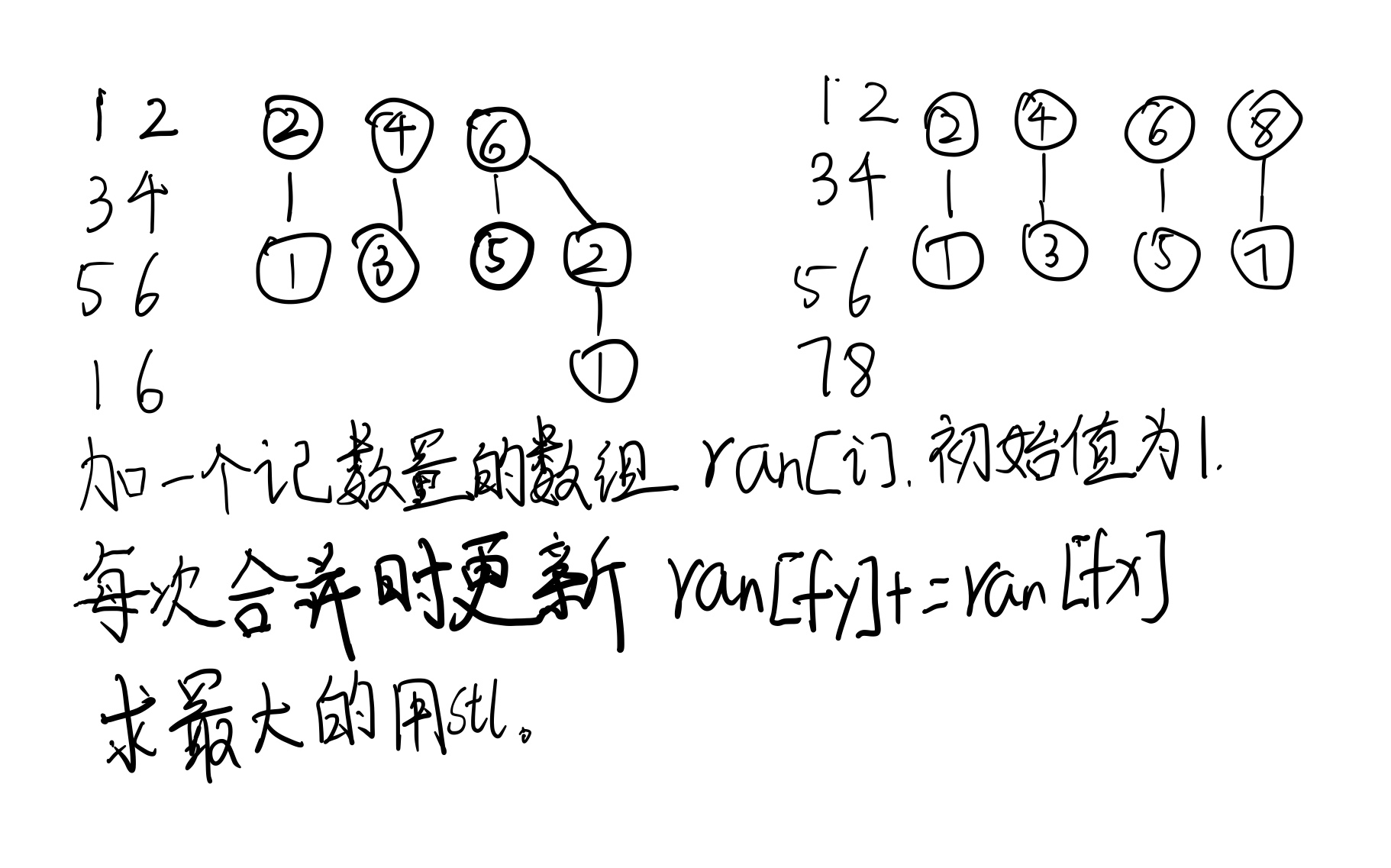
比上道龙珠题简单的多其实都差不多

AC代码：

#include <iostream>
#include <algorithm>
using namespace std;
#define maxn 110000
int N, sum;
int per[maxn], ran[maxn];
 
void init() {
    sum = 0;
    for(int i = 1; i <= maxn; ++i){
        per[i] = i;
        ran[i] = 1;
    }
}
 
int find(int x){
    int r = x;
    while( r != per[r])
        r = per[r];
    per[x] = r;
    return r;
}
 
void join (int a, int b){
    int fa = find(a);
    int fb = find(b);
    if(fa != fb){
        per[fa] = fb;
        ran[fb] += ran[fa];
        sum = max(sum, ran[fb]);
    }
}
 
int main (){
    while(scanf("%d", &N) != EOF){
        init();
        if(N == 0){
            printf("1\n");
            continue;
        }
        while(N--){
            int a, b;
            scanf("%d%d", &a, &b);
            join(a, b);
        }
        printf("%d\n", sum);
    }
    return 0;
}